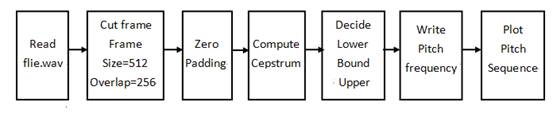
1. Low pass filter (低通濾波器)

         由於在一段人聲的音訊中，我們總會發現有凸波發生，這些凸波會造成我們對音訊的分析與處理上的困

         難度，因此我們可以用Low pass filter來降低這些凸波的影響。

　

         2.切取音框(frame)

         切取音框的方式，是一個一個點來取，音框的Size也就是所取的點數。而我們人聲的頻段介於40~1000Hz

         之間，在此我們所採用的音訊編碼格式為wav檔，它的取樣頻率為44100Hz，也就是一秒可以取44100個

         點，而我們取音框的點數為

         256、512或1024，考慮以上種種，我們選擇取512點的切音框方式，這樣可以保證人聲的一個音高週期會

         落在一個音框裡面，也方便我們做音高追蹤。

 

         3.基頻擷取

         在這個系統裡的旋律辨識，是使用音高追蹤的方法。而音高是由基頻轉換而成，下為我們所應用之基頻

         位置擷取方法。

         圖2.1是一個切出來的音框，我們可以發現，紅點所圈出來的地方正好是一個音高週期：

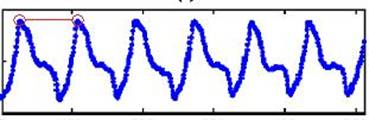
圖2.1

         而我們可以由採用的音訊編碼格式得到取樣頻率fs，也可以得到紅色點在音框中對應的Index，假設我們

         令第一、二個點的Index分別為i1、i2，我們可以得到下面數學式以求出基頻：

            Frequency=fs/(i1-i2)        (式2-1)

         上為用觀察法得到基頻，而在實現此系統時，是採用讓電腦自動算基頻的方式，因此必須發展另外的方

         法以達到自動化基頻擷取。

 

         4.基頻追蹤ACF  

     ACF(Auto Correlation Functions)是一個基於時域演算的方法，稱作自相關演算法，它的數學式如下：

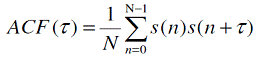         (式2-2)

 

     表示ACF就是將一段音框平移一段時間τ，然後跟原本的音框作自相關運算，就可以得到一段跟原本音框相

     同長度的序列，然後我們取這一段序列中的第一Local maximum，與第二Local maximum，這二個點發生的

     時間差，就是音高週期，也就是這一段音框的基頻所在。

圖2.2：ACF演算法示意圖

        而在切取音框時，是取512個點為一個frame，其中的overlap，也就是音框的重疊部分設定成

        frameSize/2，也就是256，這樣平移音框的時間可以設為1/2的音框時間長度，這麼做有幾個好處，首先

        我們可以確定音高週期一定會落在重疊的區域上，這樣可以保持住ACF曲線一定程度的穩定性，而且這樣

        一來所有經過ACF運算出來的音框的點數都會相同。由於overlap=frameSize/2，所以在運算時只要考慮前

        面1/2的點數，可以減少許多的運算量。

   

        但是當我們切取完音框，做完ACF得到新音框時，總會發現第一Local maximum會落在每個音框的第一個

        點，所以可將音框第一點的maximum忽略，再找區域最大值對應的Index，由所採用的音訊編碼格式的取樣

        頻率fs，可以得到下列算式計算基頻：

                Frequency=fs/(Index-1)      (式2-3)

     而人聲的頻段在40~1000Hz之間，所以我們可以將音框中由式2-4運算後小於40Hz及大於1000Hz的部分直接

     決定為這個音框的最小值，這個動作稱為Truncate，在經過Truncate後，我們就可以取音框中的最大值對

     應的Index作基頻運算了。

圖2.3：Truncate示意，綠色部分為Truncate後的音框點，藍色為被切除部分。

　

         5.倒頻譜(Cepstrum)

　　    顧名思義，就是將頻譜(Spectrum)的英文前四個字母反過來寫。是為了某些時候計算方便，先將原來信號

        轉成類似分貝的單位，在作傅立葉變換，把它視為一種新的訊號作處理。

    在字義上，倒頻譜是將信號取對數的傅立葉轉換後的新頻譜，有時候會稱頻譜的倒頻譜。倒頻譜的演算方

     式為：

                                 (式2-4)

　

     演算法：x(t) ->傅立葉轉換 ->取絕對值 ->取對數 ->反傅立葉轉換 ->倒頻譜。

　　     頻譜圖上的獨立變數是頻率，而倒頻譜圖上的獨立變數為倒頻率(quefrency)，倒頻率定義為時間的度量

         單位。舉個例子，聲音訊號取樣速率等於44100赫茲，在倒頻譜上有個很大的值在倒頻率等於100，代表

         實際上在44100/100=441赫茲有很大的值，這值出現在倒頻譜上因為頻譜上週期性出現，而頻譜上出現的

         週期與倒頻譜很大的值出現的對應倒頻率有關。

 

         6.基頻轉音高

         在擷取完基頻之後，就是將其轉為音高的時候了。轉換成音高的公式為：

pitch(x) = 69+12*log2(freq(x)/440);   (式2-5)

     所以當頻率為440時pitch為69時，相當於鋼琴的中央A(la)。

 

         7.Center clipper(中央截波器)

         我們製作中央截波器，就是要將雜訊對音訊的影響減至最小。

         下列有三種中央截波方式：

         1.y(n)=(x(n)-CL),  x(n)>=CL

               =0,          x(n)│<CL

               =(x(n)+CL),  x(n)<=-CL     (式2-6)

   

     2.y(n)=x(n),    x(n)>=CL

               =0,       x(n)│<CL

               =-x(n),   x(n)<=-CL           (式2-7)

   

     3.y(n)=1,       x(n)>=CL

               =0,       x(n)│<CL

               =-1,      x(n)<=-CL           (式2-8)

 

         其截波方式如圖所示：

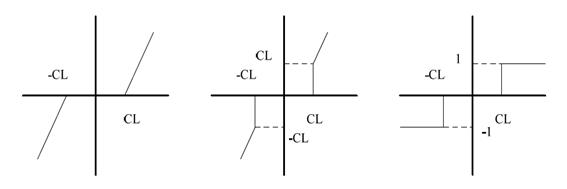
                 圖2.4：   方式1.                方式2.               方式3.

   

         其中方式3主要應用在編碼調變方面，所以在此系統中我們不會討論。

     其中CL就是decision threshold，怎麼設decision threshold ，是一個很大的難題，必須要用經驗法則

     來判斷，容後說明。

 

         8.音量

     「音量」代表聲音的強度，又稱為「力度」、「強度」(Intensity)或「能量」(Energy)，可由一個音框

     內的訊號震幅大小來類比。在計算音高時，我們要先將音訊的振福的mean值所在的縱軸位置移到0的地

     方，算式如下：

y’=y-mean(y)       (式2-9)

     完成上述動作後，接下來音量基本上有兩種運算方式：

         1.每個音框的絕對值的總和：這種方法的計算較簡單，只需要整數運算，適合用於低階平台（如微電腦

         等）。

              2.每個音框的平方值的總和，再取以 10 為底對數值，再乘以10：這種方法得到的值是以分貝

        （Decibels）為單位，是一個相對強度的值，比較符合人耳對於大小聲音的感覺。

         圖2.5的上面為方式1運算出的音量曲線，下面則為方式2：

圖2.5：音量的二種計算方式結果圖

     而輸入之音訊包含雜訊和所需的語音資訊，為了判別出可用的資訊，系統中我們將利用音量來做為判別的

     基準，將判別人沒有在唱歌時跑出來的音高曲線部分切除。

 

         9.Median filter

         Median filter顧名思義，就是利用一串序列的中位數平均，產生類似濾波器的動作，這是一個非線性的

         濾波器，又稱為平滑濾波器(smoothing filter)。

         我們使用此濾波器，目的為將運算出來的音高曲線平滑化，以方便比較。

　

         返回首頁